Ngoài các công thức tích phân đã được học thì có một cách giải khác khá hay đó là dùng máy tính casio giải. Phương pháp này gọi là casio tích phân. So với phương pháp truyền thống thì casio tích phân có tốc độ giải nhanh tới mức khác biệt.

Chuẩn bị
- Máy tính casio fx 580 các loại
- Biết bấm máy tính casio ở mức cơ bản
Bài tập vận dụng
Câu 1. Tích phân \(I = \int\limits_2^5 {\frac{{dx}}{x}} \) có giá trị bằng
A. \(3\ln 3\).
B. \(\frac{1}{3}\ln 3\).
C. \(\ln \frac{5}{2}\).
D. \(\ln \frac{2}{5}\).
Hướng dẫn giải
Cách 1: Phương pháp tự luận
\(I = \int\limits_2^5 {\frac{{dx}}{x}} = \left. {\ln \left| x \right|} \right|_2^5 = \ln 5 – \ln 2 = \ln \frac{5}{2}\).
Cách 2: Phương pháp trắc nghiệm
Bước 1: Dùng máy tính như hình bên, thu được giá trị 0,91629…
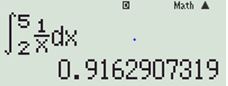
Bước 2: Lấy \({e^{0,91629…}}\) cho kết quả \(\frac{5}{2}\)

=> chọn \(\ln \frac{5}{2}\).
Cách 3: Phương pháp trắc nghiệm
Thực hiện các phép tính sau trên máy tính (đến khi thu được kết quả bằng 0 thì ngưng)
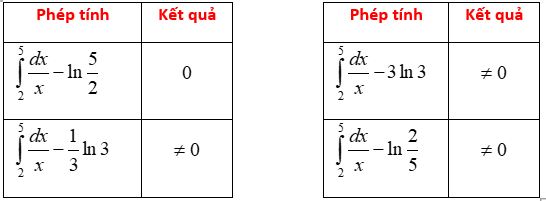
chọn $\ln \frac{5}{2}$ .
Câu 2. Tích phân \(I = \int\limits_{\frac{\pi }{3}}^{\frac{\pi }{2}} {\frac{{dx}}{{\sin x}}} \) có giá trị bằng
A. \(\frac{1}{2}\ln \frac{1}{3}\).
B. \(2\ln 3\).
C. \(\frac{1}{2}\ln 3\).
D. \(2\ln \frac{1}{3}\).
Hướng dẫn giải
Cách 1: Phương pháp tự luận
\(\begin{array}{c}I = \int\limits_{\frac{\pi }{3}}^{\frac{\pi }{2}} {\frac{{dx}}{{\sin x}}} = \int\limits_{\frac{\pi }{3}}^{\frac{\pi }{2}} {\frac{{\left( {{{\cos }^2}\frac{x}{2} + {{\sin }^2}\frac{x}{2}} \right)}}{{2\sin \frac{x}{2}\cos \frac{x}{2}}}dx} = \frac{1}{2}\int\limits_{\frac{\pi }{3}}^{\frac{\pi }{2}} {\left( {\cot \frac{x}{2} + \tan \frac{x}{2}} \right)dx} \\ = \left. {\left[ {\ln \left| {\sin \frac{x}{2}} \right| – \ln \left| {\cos \frac{x}{2}} \right|} \right]} \right|_{\frac{\pi }{3}}^{\frac{\pi }{2}}\\ = \left[ {\ln \frac{{\sqrt 2 }}{2} – \ln \frac{{\sqrt 2 }}{2}} \right] – \left[ {\ln \frac{1}{2} – \ln \frac{{\sqrt 3 }}{2}} \right]\\ = \ln \sqrt 3 .\end{array}\)
Cách 2: Phương pháp trắc nghiệm
Bước 1: Dùng máy tính như hình bên, thu được giá trị \(0,549306…\)
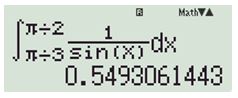
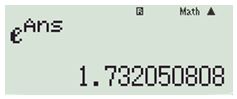
Bước 2: Lấy \({e^{0,549306…}}\) cho kết quả \(1,732050808… \approx \sqrt 3 \) chọn \(\frac{1}{2}\ln 3\).
Cách 3: Phương pháp trắc nghiệm
Thực hiện các phép tính sau trên máy tính (đến khi thu được kết quả bằng 0 thì ngưng)
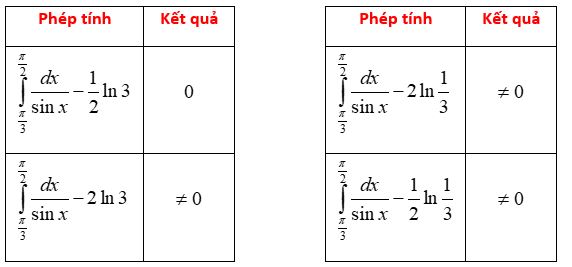
chọn $\frac{1}{2}\ln 3$ .
Nhận xét: Ở bài này cách làm bằng máy tính có vẻ nhanh hơn.
Câu 3. Nếu \(\int\limits_{ – 2}^0 {\left( {4 – {e^{ – x/2}}} \right)dx} = K – 2e\) thì giá trị của \(K\) là
A. \(12,5\).
B. \(9\).
C. \(11\).
D. \(10\).
Hướng dẫn giải
Phương pháp tự luận
\(K = \int\limits_{ – 2}^0 {\left( {4 – {e^{ – x/2}}} \right)dx} + 2e = \left. {\left( {4x + 2{e^{ – x/2}}} \right)} \right|_{ – 2}^0 + 2e = 2 – \left( { – 8 + 2e} \right) + 2e = 10\).
Phương pháp trắc nghiệm
Dùng máy tính tính \(\int\limits_{ – 2}^0 {\left( {4 – {e^{ – x/2}}} \right)dx} + 2e\) như hình bên, thu được giá trị \(K = 10\).
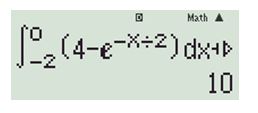
Câu 4. Tích phân \(I = \int\limits_0^1 {\frac{1}{{{x^2} – x – 2}}dx} \) có giá trị bằng
A. \(\frac{{2\ln 2}}{3}\).
B. \( – \frac{{2\ln 2}}{3}\).
C. \( – 2\ln 2\).
D. \(2\ln 2\).
Hướng dẫn giải
Phương pháp tự luận
$\begin{array}{l}\int\limits_0^1 {\frac{1}{{{x^2} – x – 2}}dx} \\ = \int\limits_0^1 {\frac{1}{{(x – 2)(x + 1)}}dx} \\ = \frac{1}{3}\int\limits_0^1 {\left[ {\frac{1}{{x – 2}} – \frac{1}{{x + 1}}} \right]dx} \\ = \frac{1}{3}\left. {\left[ {\ln \left| {x – 2} \right| – \ln \left| {x + 1} \right|} \right]} \right|_0^1 = – \frac{{2\ln 2}}{3}\end{array}$.
Học sinh có thể áp dụng công thức \(\int {\frac{1}{{(x – a)(x – b)}}dx = \frac{1}{{a – b}}\ln \left| {\frac{{x – a}}{{x – b}}} \right| + C} \) để giảm một bước tính:
\(\begin{array}{l}I = \int\limits_0^1 {\frac{1}{{{x^2} – x – 2}}dx} \\ = \int\limits_0^1 {\frac{1}{{(x – 2)(x + 1)}}dx} \\ = \frac{1}{3}\left. {\ln \left| {\frac{{x – 2}}{{x + 1}}} \right|} \right|_0^1\\ = – \frac{{2\ln 2}}{3}\end{array}\).
Phương pháp trắc nghiệm
Bước 1: Dùng máy tính như hình bên, thu được giá trị \( – 0.4620981…\)
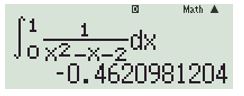
Bước 2: Loại đáp án dương \(\frac{{2\ln 2}}{3}\) và loại đáp án nhiễu “Không xác định”.
Bước 3: Chia giá trị \( – 0.4620981…\) cho \(\ln 2\), nhận được \( – \frac{2}{3}\)
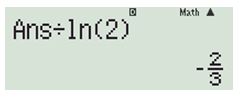
=> chọn \( – \frac{{2\ln 2}}{3}\).
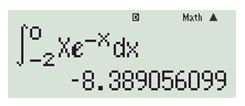
Câu 5. Tích phân \(I = \int\limits_{ – 2}^0 {x{e^{ – x}}dx} \) có giá trị bằng
A. \( – {e^2} + 1\).
B. \(3{e^2} – 1\).
C. \( – {e^2} – 1\).
D. \( – 2{e^2} + 1\).
Hướng dẫn giải
Phương pháp tự luận
Sử dụng tích phân từng phần, ta được
\(\begin{array}{c}I = \int\limits_{ – 2}^0 {x{e^{ – x}}dx} \\ = – \int\limits_{ – 2}^0 {xd\left( {{e^{ – x}}} \right)} \\ = – \left[ {\left. {\left( {x{e^{ – x}}} \right)} \right|_{ – 2}^0 – \int\limits_{ – 2}^0 {{e^{ – x}}dx} } \right]\\ = – \left. {\left( {x{e^{ – x}}} \right)} \right|_{ – 2}^0 + \int\limits_{ – 2}^0 {{e^{ – x}}dx} \\ = – \left. {\left( {x{e^{ – x}}} \right)} \right|_{ – 2}^0 – \left. {\left( {{e^{ – x}}} \right)} \right|_{ – 2}^0\\ = – {e^2} – 1.\end{array}\)
Phương pháp trắc nghiệm
Dùng máy tính tính \(\int\limits_{ – 2}^0 {x{e^{ – x}}dx} \) như hình bên, thu được kết quả như hình bên. Loại được đáp án \(3{e^2} – 1\). Sau đó thử từng đáp án còn lại để tìm ra kết quả.
Câu 6. Cho tích phân: \(I = \int\limits_1^e {\frac{{\sqrt {1 – \ln x} }}{{2x}}dx} \).Đặt \(u = \sqrt {1 – \ln x} \).Khi đó \(I\) bằng
A. \(I = \int\limits_1^0 {{u^2}du} \).
B. \(I = – \int\limits_1^0 {{u^2}du} \).
C. \(I = \int\limits_1^0 {\frac{{{u^2}}}{2}du} \).
D. \(I = – \int\limits_0^1 {{u^2}du} \).
Hướng dẫn giải
[Phương pháp tự luận]
Đặt \(u = \sqrt {1 – \ln x} \Rightarrow {u^2} = 1 – \ln x\) \( \Rightarrow \frac{{dx}}{x} = – 2udu\). Với \(x = 1 \Rightarrow u = 1\),\(x = e \Rightarrow u = 0\).
Khi đó \(I = – \int\limits_1^0 {{u^2}du} \).
[Phương pháp trắc nghiệm]
- Bước 1: Bấm máy tính để tính \(\int\limits_1^e {\frac{{\sqrt {1 – \ln x} }}{{2x}}dx} \)
- Bước 2: Bấm SHIFT STO A để lưu vào biến A.
- Bước 3: Bấm\(A – \left( { – \int\limits_1^0 {{u^2}du} } \right) = 0\). Vậy đáp án là A.
Câu 7. Cho hàm số \(f\) liên tục trên đoạn \([0;6]\). Nếu \(\int\limits_1^5 {f(x)dx} = 2\) và \(\int\limits_1^3 {f(x)dx} = 7\) thì \(\int\limits_3^5 {f(x)dx} \) có giá trị bằng
A. \(5\).
B. \( – 5\).
C. \(9\).
D. \( – 9\).
Hướng dẫn giải
\(\int\limits_3^5 {f(x)dx} = \int\limits_3^1 {f(x)dx} + \int\limits_1^5 {f(x)dx} = – \int\limits_1^3 {f(x)dx} + \int\limits_1^5 {f(x)dx} = – 7 + 2 = – 5\).
Câu 8. Trong các phép tính sau đây, phép tính nào sai?
A. $\int\limits_1^3 {{e^x}dx} = \left. {\left( {{e^x}} \right)} \right|_1^3$.
B. $\int\limits_{ – 3}^{ – 2} {\frac{1}{x}dx} = \left. {\left( {\ln x} \right)} \right|_{ – 3}^{ – 2}$.
C. $\int\limits_\pi ^{2\pi } {\cos xdx} = \left. {\left( {\sin x} \right)} \right|_\pi ^{2\pi }$.
D. $\int\limits_1^2 {\left( {x + 1} \right)dx} = \left. {\left( {\frac{{{x^2}}}{2} + x} \right)} \right|_1^2$.
Hướng dẫn giải
Phép tính $\int\limits_{ – 3}^{ – 2} {\frac{1}{x}dx} = \left. {\left( {\ln x} \right)} \right|_{ – 3}^{ – 2}$ là sai. Phép tính đúng là $\int\limits_{ – 3}^{ – 2} {\frac{1}{x}dx} = \left. {\left( {\ln \left| x \right|} \right)} \right|_{ – 3}^{ – 2}$.
Câu 9. Giả sử \(F\) là một nguyên hàm của hàm số \(y = {x^6}{\sin ^5}x\) trên khoảng \((0; + \infty )\). Khi đó \(\int\limits_1^2 {{x^6}{{\sin }^5}xdx} \) có giá trị bằng
A. \(F(2) – F(1)\).
B. \( – F(1)\).
C. \(F(2)\).
D. \(F(1) – F(2)\).
Hướng dẫn giải
Áp dụng công thức \(\int\limits_a^b {f(x)dx} = F(b) – F(a)\), trong đó \(F\) là một nguyên hàm của \(f\) trên đoạn \([a;b]\), ta có \(\int\limits_1^2 {{x^6}{{\sin }^5}xdx} = F(2) – F(1)\).
Câu 10. Trong các hàm số dưới đây, hàm số nào có tích phân trên đoạn \([0;\pi ]\) đạt giá trị bằng \(0\)?
A. \(f(x) = \cos 3x\).\(f(x) = \sin 3x\)
B. \(f(x) = \cos 4x\).\(f(x) = \sin 3x\)
C. \(f(x) = \cos \left( {\frac{x}{4} + \frac{\pi }{2}} \right)\).
D. \(f(x) = \sin \left( {\frac{x}{4} + \frac{\pi }{2}} \right)\).
Hướng dẫn giải
Tính tích phân cho từng hàm số trong các đáp án:
- $\int\limits_0^\pi {\cos 3xdx} = \left. {\frac{1}{3}\sin 3x} \right|_0^\pi = 0$
- $\int\limits_0^\pi {\sin 3xdx} = – \left. {\frac{1}{3}\cos 3x} \right|_0^\pi = 2$
- $\int\limits_0^\pi {\cos \left( {\frac{x}{4} + \frac{\pi }{2}} \right)dx} = \left. {4\sin \left( {\frac{x}{4} + \frac{\pi }{2}} \right)} \right|_0^\pi = 2\left( {\sqrt 2 – 2} \right)$
- $\int\limits_0^\pi {\sin \left( {\frac{x}{4} + \frac{\pi }{2}} \right)dx} = \left. { – 4\cos \left( {\frac{x}{4} + \frac{\pi }{2}} \right)} \right|_0^\pi = 2\sqrt 2 $.
Vậy chọn \(f(x) = \cos 3x\).
Hy vọng với cách giải khá hay này sẽ giúp học sinh tăng tốc giải các bài tập trắc nghiệm và đạt kết quả cao. Chúc bạn luyện được tuyệt kĩ casio tích phân cực hay này.