Không phải cứ vận dụng bảng nguyên hàm là ta có thể giải được mọi bài. Hôm nay, admin giới thiệu với em phương pháp nguyên hàm từng phần. Đây là phương pháp rất hiệu quả nếu học sinh biết cách vận dụng thành thạo. Nó được coi là 1 trong những phương pháp giải nguyên hàm được thầy cô mong đợi và tin dùng nhất hiện nay.

Phương pháp
Nếu hai hàm số u = u(x) và v = v(x) có đạo hàm liên tục trên tập xác định k thì
\(\int {u\left( x \right)v’\left( x \right)d{\rm{x}} = u\left( x \right)v\left( x \right) – } \int {u’\left( x \right)v\left( x \right)d{\rm{x}}} \)
Hay \(\int {u{\rm{d}}v = uv – \int {v{\rm{d}}u} } \)
Bài tập vận dụng
Bài tập 1:. Tính \(F\left( x \right) = \int {(2x – 1){e^{1 – x}}dx} = {e^{1 – x}}(Ax + B) + C\). Giá trị của biểu thức \(A + B\) bằng:

Bài tập 2: Tính \(F(x) = \int {{e^x}\cos xdx} = {e^x}(A\cos x + B\sin x) + C\). Giá trị của biểu thức \(A + B\) bằng
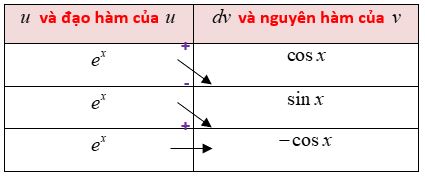
Do đó \(F(x) = {e^x}\sin x + {e^x}\cos x – F(x) + {C_1}\) hay \(F(x) = \frac{1}{2}\left( {{e^x}\sin x + {e^x}\cos x} \right) + C\).
Vậy \(A + B = 1\).
Bài tập 3: Tính \(F(x) = \int {2x{{(3x – 2)}^6}dx} = A{(3x – 2)^8} + Bx{(3x – 2)^7} + C\). Giá trị của biểu thức \(12A + 11B\) là

Do đó \(F(x) = \frac{2}{{21}}x{(3x – 2)^7} – \frac{1}{{252}}{(3x – 2)^8} + C\).
Vậy \(12A + 11B = 1\).
Hy vọng với phương pháp nguyên hàm từng phần kèm lời giải chi tiết bài tập đã giúp em học thêm được phương pháp hiệu quả cao trong giải bài tập.