Dựa vào năng lượng toàn phần để giải các bài tập về con lắc lò xo và con lắc đơn là một cách hay được nhiều hs dùng. Để hiểu hơn thì bài viết này sẽ giới thiệu về năng lượng toàn phần của con lắc lò xo. Đây là 1 trong những phương pháp rất hay giúp bạn giải bài tập hiệu quả. Dưới đây giới thiệu 4 bài tập trắc nghiệm ứng với 4 dạng bài:
Công thức cần nhớ
Dưới đây là những công thức về năng lượng toàn phần bạn cần nhớ
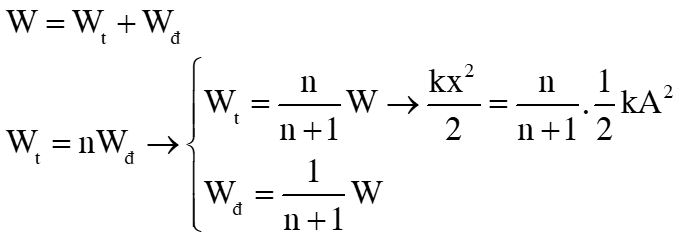
Trắc nghiệm năng lượng toàn phần
Câu 1. Kích thích một chất điểm để nó dao động điều hòa với chu kỳ T và biên độ là A. Hỏi khoảng thời gian giữa hai lần liên tiết thế năng bằng với động năng là bao nhiêu?
A. 3T/4
B. 0,125T
C. 0,42T
D. 0,25T
Trả lời
Ta biết rằng Năng lượng toàn phần bằng động năng và thế năng biến thiên. Trong đó động năng và thế năng biến thiên với chu kì là T’ = 0,25T nên khoảng thời gian giữa 2 lần liên tiếp thế năng bằng với động năng tương ứng là
t = T’/2 = T/4 = 0,25T
Đáp án là D.
Câu 2. Kích thích chất điểm để nó dao động với biên độ A và chu kì là T. Tại thời điểm t = 0, vật đang ở VTCB.Hỏi khoảng thời gian ngắn nhất từ lúc t = 0 đến lúc thế năng bằng với động năng là bao nhiêu
A. 0,25T
B. 0,125T
C. 0,123T
D. 0,356T
Trả lời
Ta có công thức tổng quát khi ${W_t} = n{W_d} \Rightarrow \left| x \right| = A\sqrt {\frac{n}{{n + 1}}} $
Từ biểu thức trên ta thấy: $n = 1 \Rightarrow \left| x \right| = A\sqrt {\frac{n}{{n + 1}}} = A\sqrt {\frac{1}{{1 + 1}}} = \frac{{A\sqrt 2 }}{2}$
+ Thời gian ngắn nhất cần tìm là $\varphi = \omega .{t_{\min }} \to {t_{\min }} = \frac{\varphi }{\omega } = \frac{{\frac{\pi }{4}}}{{\frac{{2\pi }}{T}}} = \frac{T}{8}.$
Đáp án chính xác là B
Câu 3. Chất điểm có khối lượng m = 1000 g, kích thích cho dao động điều hòa với phương trình x = A.cos(4t) cm, với thời gian t tính bằng giây. Người ta thấy rằng khi vật đi được quãng đường lớn nhất trong T/4 là 0,1√2 m. Năng lượng toàn phần của vật bằng
A. 0,08 J.
B. 0,142 J.
C. 0,111 J.
D. 0,124 J.
Trả lời
Theo đề bài, quáng đường lớn nhất: ${S_{m{\rm{ax}}}} = 0,1\sqrt 2 \left( m \right)$
Áp dụng công thức tìm quãng đường lớn nhất khi vật đi dược khoảng thời gian t = T/4: ${S_{m{\rm{ax}}}} = 2A\sin \frac{{\Delta \varphi }}{2} = 2A\sin \frac{{\frac{{2\pi }}{T}.\frac{T}{4}}}{2} = \sqrt 2 .A$
Từ 2 dữ kiện trên, ta suy ra được: $A = 0,1\left( m \right) \to {\rm{W}} = \frac{1}{2}m{\omega ^2}{A^2} = 0,08\left( J \right)$
Chọn đáp án A.
Câu 4. Một con lắc lò xo được đặt nằm nghiêng với góc 300. Biết rằng lò xo có độ cứng 100 N/m và chất điểm có khối lượng 1 kg. Khi vật đang ở VTCB thì tác động vào vật theo phương lò xo làm nó giãn 8 cm rồi thả nhẹ để nó dao động điều hòa. Hãy xác định năng lượng toàn phần của vật nặng? Lấy gia tốc rơi tự do g = 10 m/s2.
A. 0,045 J.
B. 1,24 J.
C. 5,254 J.
D. 0,2356 J.
Trả lời
Trong phần lý thuyết ta đã biết công thức về vị trí cân bằng con lắc nằm nghiêm: ${k\Delta {\ell _0} = mg\sin \alpha }$
Bằng biến đổi toán học: ${\Delta {\ell _0} = \frac{{mg\sin \alpha }}{k} = 0,05\left( m \right)}$
Khi đó biên độ dao động con lắc: ${A = \Delta {\ell _{m{\rm{ax}}}} – \Delta {\ell _0} = 0,03\left( m \right)}$
Lúc này ta tính được Năng lượng toàn phần con lắc: ${{{\rm{W}}_{d\max }} = \frac{1}{2}k{A^2} = 0,045\left( J \right)}$
Chọn đáp án A.
Bài viết trên đã phần nào giúp bạn hiểu năng lượng toàn phần của con lắc lò xo. Hy vọng sẽ giúp bạn học tốt hơn vật lý lớp 12.