Giống con lắc lò xo, chu kì con lắc đơn cũng có biểu thức tương tự. Bài viết này sẽ hướng dẫn chi tiết từ công thức căn bản đến giải thích các đại lượng, đơn vị và bài tập ví dụ để hiểu sâu
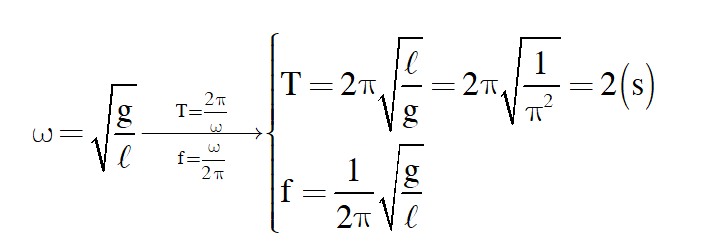
Cơ sở lý thuyết
Ta biết tần số góc của con lắc đơn được xác định theo công thức: $\omega = \sqrt {\frac{g}{\ell }} $
Mà ${T = \frac{{2\pi }}{\omega }}$ nên chu kì dao con lắc đơn sẽ là: $T = 2\pi \sqrt {\frac{\ell }{g}} $
Giải thích:
- Gia tốc rơi tự do là g ( đơn vị m/s2)
- l là chiều dài sợi dậy con lắc ( đơn vị là m)
- T là chu kì con lắc đơn (đơn vị là s)
Ví dụ chu kì con lắc đơn
Câu 1. Một con lắc đơn có sợi dây dài ℓ = 1 m, con lắc đang dao động tại nơi có gia tốc trọng trường g = π2. Nếu con lắc dao động điều hòa thì chu kì dao động của nó là?
Hướng dẫn giải
Vì con lắc dao động điều hòa nên chu kì nó được xác định theo công thức $T = 2\pi \sqrt {\frac{\ell }{g}} $
Thay số vào: $T = 2\pi \sqrt {\frac{\ell }{g}} = 2\pi \sqrt {\frac{1}{{{\pi ^2}}}} = 2\left( s \right)$
Đáp án là T = 2s.
Câu 2. Một con lắc đơn dao động điều hòa có chiều dài ℓ, nếu như ta cắt bớt 19 cm từ chiều dài con lắc thì ta thấy chu kì dao động con lắc thay đổi 0,9 lần so với ban đầu. Hỏi chiều dài của con lắc lúc đầu là bao nhiêu?
Hướng dẫn giải
Theo đề thì chiều dài con lắc $\ell ‘ = \ell – 0,19$
Khi đó chu kì con lắc đơn $\frac{{T’}}{T} = 0,9 \to \sqrt {\frac{{\ell ‘}}{\ell }} = 0,9$
Từ 2 biểu thức trên ta có: $0,{9^2}\ell = \ell – 0,19 \to \ell = 1\left( m \right) = 100\left( {cm} \right)$
Kết quả là chiều dài con lắc đơn khi chưa bị cắt dài 100 cm
Câu 3. Khảo sát hai con lắc đơn dao động điều hòa: con lắc thứ nhất có chiều dài ℓ1 thì chu kì là T1 = 0,8s. Con lắc thứ 2 có chiều dài ℓ2 thì chu kì dao động là T2 = 0,6s. Giờ con lắc có chiều dài ℓ 1 + ℓ2 thì chu kì có độ lớn là nhiêu?
Hướng dẫn giải
Ta sử dụng một vài biến đối toán học cơ bản như sau:
$\begin{array}{l}T = 2\pi \sqrt {\frac{\ell }{g}} \to \ell = {\left( {\frac{T}{{2\pi }}} \right)^2}.g\\\to \left\{ \begin{array}{l}{\ell _1} = {\left( {\frac{{{T_1}}}{{2\pi }}} \right)^2}.g\\{\ell _2} = {\left( {\frac{{{T_2}}}{{2\pi }}} \right)^2}.g\\\ell = {\left( {\frac{T}{{2\pi }}} \right)^2}.g\\\ell = {\ell _1} + {\ell _2}\end{array} \right. \to {\left( {\frac{T}{{2\pi }}} \right)^2}.g = {\left( {\frac{{{T_2}}}{{2\pi }}} \right)^2}.g + {\left( {\frac{{{T_1}}}{{2\pi }}} \right)^2}.g\\\to T = \sqrt {T_1^2 + T_2^2} = \sqrt {0,{8^2} + 0,{6^2}} = 1\left( s \right).\end{array}$
Vậy chu kì con lắc đơn là: $T = \sqrt {T_1^2 + T_2^2} = \sqrt {0,{8^2} + 0,{6^2}} = 1\left( s \right).$
Hy vọng với hướng dẫn cơ bản về lý thuyết kèm bài tập minh họa công thức tính chu kì con lắc đơn sẽ giúp bạn học hiệu quả. Mọi bình luận vui lòng để lại dưới đây.