Muốn học tốt bài lực đàn hồi con lắc lò xo thì bạn phải xem lại chu kì dao động đã được học tư bài trước, độ biến dạng đàn hồi của con lắc lò xo được học từ lớp 10.
Lực đàn hồi là gì?
Lực đàn hồi Fđh là lực xuất hiện khi lò xo có sự biến dạng, lực này sẽ đưa vật về vị trí lò xo có chiều dài tự nhiên ℓ0.
Cơ sở lý thuyết
Biểu thức lực đàn hồi
Fđh = k(x + ∆ℓ0) = mω2(x + ∆ℓ0)
Giải thích:
- Hệ số đàn hồi k (N/m)
- Li độ dao động x (m)
- Độ biến dạng tự nhiên ∆ℓ0 (m)
- Khống lượng quả nặng m (kg)
- Tần số góc ω (rad/s)
Chiều lực tác dụng
Trường hợp 1: Con lắc lò xo nằm ngang thì
- ∆ℓ0 = 0 =>Fđh = k(x)
Trường hợp 2: Con lắc lò xo treo thẳng đứng
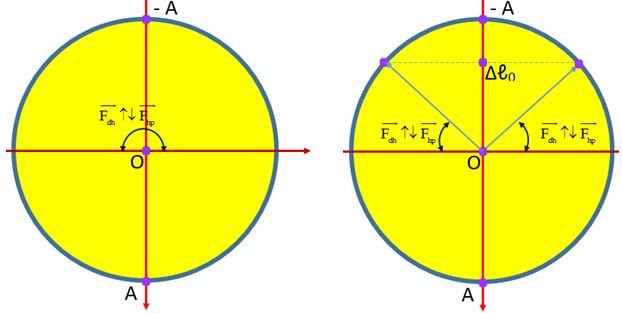
- Nếu A ≤ ∆ℓ0 thì ℓ0 + ∆ℓ0 – A ≤ ℓ ≤ ℓ0 + ∆ℓ0
- Nếu A > ∆ℓ0 thì ℓ0 ≤ ℓ ≤ ℓ0 + ∆ℓ0
Bài tập vận dụng
Câu 1: Một vật khối lượng 1 kg dao động điều hòa với phương trình: x = 10cos(πt) (cm). Lực phục hồi (lực kéo về) cực đại tác dụng lên vật
A. 1 N.
B. 4 N.
C. 10 N.
D. π N.
Hướng dẫn giải
$\left. \begin{array}{l} m = 1kg\\ \omega = \pi \left( {\frac{{rad}}{s}} \right)\\ A = 10\left( {cm} \right) = 0,1\left( m \right) \end{array} \right\} \to {F_{hp\max }} = m{\omega ^2}A = 1\left( N \right)$
Chọn A
Câu 2: Một lò xo có k = 20N/m treo thẳng đứng, gắn vào lò xo một vật có khối lượng m=200g. Từ vị trí cân bằng, đưa vật lên một đoạn 5cm rồi buông nhẹ. Lấy g = 10m/s2. Chiều dương hướng xuống. Giá trị cực đại của lực hồi phục và lực đàn hồi là
A. 1 N, 2 N.
B. 2 N, 3 N.
C. 2 N, 5 N.
D. 1 N, 3N.
Hướng dẫn giải
$\begin{array}{l} \Delta {\ell _0} = \frac{{mg}}{k} = \frac{{0,2.10}}{{20}} = 0,1\left( m \right) = 10\left( {cm} \right) \to \Delta \ell = 5\left( m \right)\\ \to A = \left| {\Delta \ell – \Delta {\ell _0}} \right| = 5\left( {cm} \right) = 0,05\left( m \right)\\ \Delta {\ell _0} > A \to \left\{ \begin{array}{l} {F_{\min }} = k\left( {\Delta {\ell _0} – A} \right) = 20.\left( {0,1 – 0,05} \right) = 1\left( N \right)\\ {F_{\max }} = k\left( {\Delta {\ell _0} + A} \right) = 20.\left( {0,1 + 0,05} \right) = 3\left( N \right) \end{array} \right. \end{array}$
Chọn đáp án D
Câu 3: Một vật khối lượng 1 kg dao động điều hòa với phương trình: x = 10cos(πt) (cm). Lực phục hồi (lực kéo về) tác dụng lên vật vào thời điểm 0,5s là
A. 0 N.
B. 1 N.
C. 3 N.
D. 10 N.
Hướng dẫn giải
$\left. \begin{array}{l} t = 0,5\left( s \right) \to x = 10\cos \left( {\pi .0,5} \right) = 0\\ m = 1kg\\ \omega = \pi \left( {\frac{{rad}}{s}} \right) \end{array} \right\} \to {F_{hp\max }} = m{\omega ^2}x = 0\left( N \right)$
Chọn A
Câu 4: Con lắc lò xo treo thẳng đứng, lò xo có khối lượng không đáng kể. Hòn bi đang ở vị trí cân bằng thì được kéo xuống dưới theo phương thẳng đứng một đoạn 3cm rồi thả ra cho nó dao động. Hòn bi thực hiện 50 dao động mất 20s. Cho g = π2 = 10m/s2. Tỉ số độ lớn lực đàn hồi cực đại và lực đàn hồi cực tiểu của lò xo khi dao động là
A. 5.
B. 4.
C. 3.
D. 7.
Hướng dẫn giải
$\begin{array}{l} A = 3\left( {cm} \right);t = NT\\ \to T = \frac{t}{N} = \frac{{20}}{{50}} = 0,4\left( s \right)\\ \to T = 2\pi .\sqrt {\frac{{\Delta {\ell _0}}}{g}} \\ \to \Delta {\ell _0} = 0,04\left( m \right) > A\\ \to \frac{{{F_{\max }}}}{{{F_{\min }}}} = \frac{{\Delta {\ell _0} + A}}{{\Delta {\ell _0} – A}} = 7 \end{array}$
Câu 5: Một chất điểm có khối lượng m = 50g dao động điều hoà theo phương ngang trên đoạn thẳng MN = 8cm với tần số f = 5 Hz. Khi t = 0 chất điểm qua vị trí cân bằng theo chiều dương. Lấy π2 = 10. Ở thời điểm t = 1/12 s, lực gây ra chuyển động của chất điểm có độ lớn là
A. 10 N.
B. $\sqrt 3 $N.
C. 1 N.
D. $10\sqrt 3 $ N.
Hướng dẫn giải
$\begin{array}{l} \left. \begin{array}{l} \omega = 2\pi f = 10\pi \left( {\frac{{rad}}{s}} \right)\\ MN = 2A = 8\left( {cm} \right) \to A = 4\left( {cm} \right)\\ t = 0 \to \left\{ \begin{array}{l} x = 0\\ v > 0 \end{array} \right. \to \left\{ \begin{array}{l} 0 = \cos \varphi \\ \sin \varphi < 0 \end{array} \right. \to \varphi = – \frac{\pi }{2} \end{array} \right\} \to x = 4\cos \left( {10\pi t – \frac{\pi }{2}} \right)\left( {cm} \right)\\ t = \frac{1}{{12}}\left( s \right) \to x = 4\cos \left( {10\pi .\frac{1}{{12}} – \frac{\pi }{2}} \right) = 2\left( {cm} \right)\\ F = m{\omega ^2}x = 0,05.{\left( {10\pi } \right)^2}.0,02 = 1\left( N \right) \end{array}$