Tiếp theo loạt bài về ứng dụng tích phân, bài viết này giới thiệu về Ứng dụng tích phân tính thể tích khối tròn xoay. Đây là chủ đề khó, đòi hỏi phải có kiến thức nền tốt. Em nào chưa xem về ứng dụng tích phân tính diện tích hình phẳng thì xem trước khi học bài này. Ai đã xem thì chúng ta bắt đầu nào
Cơ sở lý thuyết
Trường hợp 1
Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường y = f(x), y = 0, x = a và x = b với (a <b) quay quanh trục Ox là \(V = \pi \int\limits_a^b {{f^2}(x)dx} \).
Trường hợp 2
Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường y = f(x), y = g(x), x = a và x = b với (a <b) quay quanh trục Ox là \(V = \pi \int\limits_a^b {\left| {{f^2}(x) – {g^2}(x)} \right|dx} \).
Bài tập vận dụng
Câu 1. Cho hình phẳng giới hạn bởi các đường \(y = {x^3} + 1,\,\,y = 0,\,\,x = 0,\,\,x = 1\) quay xung quanh trục Ox. Thể tích của khối tròn xoay tạo thành bằng:
A. $\frac{{79\pi }}{{63}}$
B. $\frac{{23\pi }}{{14}}$
C. $\frac{{5\pi }}{4}$
D. $9\pi $
Hướng dẫn giải
Theo công thức ta có thể tích của khối tròn xoay cần tính là:
\(V = \pi \int\limits_0^1 {{{({x^3} + 1)}^2}dx = \frac{{23\pi }}{{14}}.} \)
Câu 2. Cho hình phẳng giới hạn bởi các đường \(y = \sqrt {1 – {x^2}} ,\,\,y = 0\) quay xung quanh trục Ox. Thể tích của khối tròn xoay tạo thành bằng:
A. \(\frac{{3\pi }}{2}\)
B. \(\frac{{2\pi }}{3}\)
C. \(\frac{\pi }{2}\)
D. \(\frac{4}{3}\pi \)
Hướng dẫn giải
Giao điểm của hai đường \(y = \sqrt {1 – {x^2}} \)và \(y = 0\) là \(B( – 1;0)\)và \(A(1;0)\). Theo công thức ta có thể tích của khối tròn xoay cần tính là: \(V = \pi \int\limits_{ – 1}^1 {(1 – {x^2})dx = \frac{{4\pi }}{3}.} \)
Câu 3. Thể tích khối tròn xoay trong không gian Oxyz giới hạn bởi hai mặt phẳng \(x = 0;\;x = \pi \) và có thiết diện cắt bởi mặt phẳng vuông góc với Ox tại điểm \((x;0;0)\)bất kỳ là đường tròn bán kính \(\sqrt {\sin x} \) là:
A. \(V = 2.\)
B. \(V = \pi .\)
C. \(V = 4\pi .\)
D. \(V = 2\pi .\)
Hướng dẫn giải
Khối tròn xoay trong đề bài có được bằng cách quay hình phẳng tạo bởi các đường \(x = 0;\;x = \pi ;\;y = \sqrt {\sin x} ;\;Ox\)quay trục Ox.
Theo công thức ta có thể tích của khối tròn xoay cần tính là: \(V = \pi \int\limits_0^\pi {\sin {\rm{x}}dx = 2\pi .} \)
Câu 4. Cho hình phẳng giới hạn bởi các đường \(y = 1 + \sqrt x {\rm{,}}\,\,{\rm{Ox,}}\,\,{\rm{x = 0,}}\,\,{\rm{x = 4}}\) quay xung quanh trục Ox. Thể tích của khối tròn xoay tạo thành bằng:
A. \({\pi ^2}\frac{{28}}{3}\)
B. \(\pi .\frac{{68}}{3}\)
C. \(\pi \frac{{28}}{3}\)
D. \({\pi ^2}.\frac{{68}}{3}\)
Hướng dẫn giải
Theo công thức ta có thể tích của khối tròn xoay cần tính là: \(V = \int\limits_0^4 {\pi .{{(1 + \sqrt x )}^2}dx} = \frac{{68\pi }}{3}.\)
Câu 5. Cho hình phẳng giới hạn bởi các đường \(y = a.{x^2},\,\,y = bx\,\,(a,b \ne 0)\) quay xung quanh trục Ox. Thể tích của khối tròn xoay tạo thành bằng:
A. \(V = \pi .\frac{{{b^3}}}{{{a^3}}}\left( {\frac{1}{3} – \frac{1}{5}} \right)\)
B. \(V = \pi .\frac{{{b^5}}}{{5{a^3}}}\)
C. \(V = \pi .\frac{{{b^5}}}{{3{a^3}}}\)
D. \(V = \pi .\frac{{{b^5}}}{{{a^3}}}\left( {\frac{1}{3} – \frac{1}{5}} \right)\)
Hướng dẫn giải
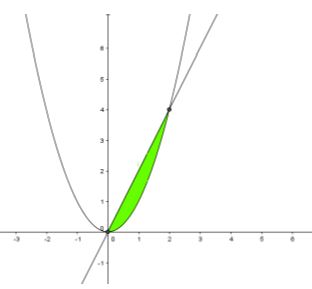
Tọa độ giao điểm của hai đường \(y = a{x^2}\) và \(y = bx\) là các điểm \(O(0;0)\) và \(A(\frac{b}{a};\frac{{{b^2}}}{a})\). Vậy thể tích của khối tròn xoay cần tính là: \(V = \int\limits_0^{\frac{b}{a}} {\pi .{b^2}{x^2}dx – \int\limits_0^{\frac{b}{a}} {\pi .{a^2}{x^4}dx} = \pi .\frac{{{b^5}}}{{{a^3}}}(\frac{1}{3} – \frac{1}{5}).} \)
Câu 6. Cho hình phẳng giới hạn bởi các đường \(y = x.\sqrt {\ln x} ,\,\,y = 0,\,\,x = e\) quay xung quanh trục Ox. Thể tích của khối tròn xoay tạo thành bằng:
A. $\pi .\frac{{4{e^3} + 1}}{9}$
B. $\pi .\frac{{4{e^3} – 1}}{9}$
C. $\pi .\frac{{2{e^3} + 1}}{9}$
D. $\pi .\frac{{2{e^3} – 1}}{9}$
Hướng dẫn giải
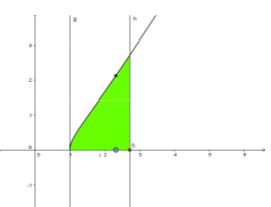
Tọa độ giao điểm của đường \(x = e\) với \(y = x\sqrt {\ln x} \) là điểm \(C(3;3)\). Tọa độ giao điểm của đường \(y = x\sqrt {\ln x} \) với \(y = 0\) là \(A(1;0)\). Vậy thể tích của khối tròn xoay cần tính là: $V = \int\limits_1^e {\pi .{x^2}\ln xdx = \pi .} \frac{{2{e^3} + 1}}{9}.$
Câu 7. Một vật có kích thước và hình dáng như hình vẽ dưới đây. Đáy là hình tròn giới hạn bởi đường tròn\({x^2} + {y^2} = 16\)(nằm trong mặt phẳng Oxy), cắt vật bởi các mặt phẳng vuông góc với trục Ox ta được thiết diện là tam giác đều. Thể tích của vật thể là:
A. $V = \frac{{256\sqrt 3 }}{3}.$
B. $V = \frac{{256}}{3}.$
C. $V = \frac{{32\sqrt 3 }}{3}.$
D. $V = \frac{{32}}{3}.$
Hướng dẫn giải
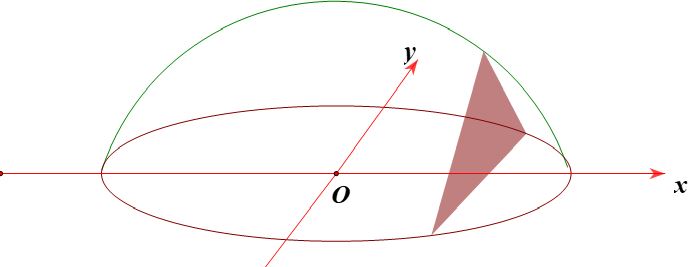
Giao điểm của thiết diện và Ox là H. Đặt \(OH = x\) suy ra cạnh của thiết diện là \(2\sqrt {16 – {x^2}} \). Diện tích thiết diện tại H là \(S(x) = \frac{{\sqrt 3 }}{4}4(16 – {x^2})\).
Vậy thể tích của vật thể là \(V = \int\limits_{ – 4}^4 {\sqrt 3 (16 – {x^2})dx = \frac{{256\sqrt 3 }}{3}.} \)
Câu 8. Cho hình phẳng giới hạn bởi các đường \(y = 2{x^2},\,\,{y^2} = 4x\) quay xung quanh trục Ox. Thể tích của khối tròn xoay tạo thành bằng:
A. \(V = \frac{{88\pi }}{5}.\)
B. \(V = \frac{{9\pi }}{{70}}.\)
C. \(V = \frac{{4\pi }}{3}.\)
D. \(V = \frac{{6\pi }}{5}.\)
Hướng dẫn giải
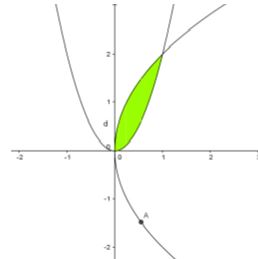
Với $x \in \left[ {0;2} \right]$ thì \({y^2} = 4x \Leftrightarrow y = \sqrt {4x} \)
Tọa độ giao điểm của đường \(y = 2{x^2}\) với \({y^2} = 4x\) là các điểm \(O(0;0)\) và \(A(1;2)\). Vậy thể tích của khối tròn xoay cần tính là: $V = \int\limits_0^1 {\pi .4xdx – \int\limits_0^1 {\pi .4{x^4}dx} = \pi .} \frac{6}{5}.$
Trên là hướng dẫn sử dụng tích phân để giải các bài toán tính diện tích khối tròn xoay. Mọi thắc mắc vui lòng để lại bình luận bên dưới.