Bên cạnh các phương pháp giải tích phân, bảng công thức tích phân thì học sinh cần học tốt phần ứng dụng tích phân để tính diện tích hình phẳng. Bài này khá quan trọng bởi nó xuất hiện nhiều trong đề thi minh họa năm 2020, đề thi chính thức của bộ qua các năm 2019, 2018, 2017, …..
Cơ sở lý thuyết
Trường hợp 1
Cho hai hàm số f(x) và g(x) liên tục trên đoạn [a; b]. Diện tích hình phẳng giới hạn bởi các đường y = f(x), y = g(x), x = a, x = b là \(S = \int\limits_a^b {\left| {f(x) – g(x)} \right|dx} \).
Phương pháp giải toán
- Giải phương trình f(x) = g(x) (1)
- Nếu (1) vô nghiệm thì \(S = \left| {\int\limits_a^b {\left( {f(x) – g(x)} \right)dx} } \right|\).
- Nếu (1) có nghiệm thuộc [a, b]. giả sử α thì
\(S = \left| {\int\limits_a^\alpha {\left( {f(x) – g(x)} \right)dx} } \right| + \left| {\int\limits_\alpha ^b {\left( {f(x) – g(x)} \right)dx} } \right|\)
Chú ý: Có thể lập bảng xét dấu hàm số f(x) – g(x) trên đoạn [a; b] rồi dựa vào bảng xét dấu để tính tích phân.
Trường hợp 2
Cho hai hàm số f(x) và g(x) liên tục trên đoạn [a; b]. Diện tích hình phẳng giới hạn bởi các đường y = f(x), y = g(x) là \(S = \int\limits_\alpha ^\beta {\left| {f(x) – g(x)} \right|dx} \). Trong đó α, β là nghiệm nhỏ nhất và lớn nhất của phương trình f(x) = g(x) với (a ≤ α < β ≤ b).
Phương pháp giải toán
- Bước 1. Giải phương trình f(x) = g(x) tìm các giá trị α, β.
- Bước 2. Tính \(S = \int\limits_\alpha ^\beta {\left| {f(x) – g(x)} \right|dx} \)như trường hợp 1.
Bài tập vận dụng
Câu 1. Hình phẳng (H) được giới hạn bởi đồ thị hai hàm số \(y = \left| {{x^2} – 4x + 3} \right|,\,\,y = x + 3\). Diện tích của (H) bằng
A. \(\frac{{108}}{5}\)
B. \(\frac{{109}}{5}\)
C. \(\frac{{109}}{6}\)
D. \(\frac{{119}}{6}\)
Hướng dẫn giải
Xét pt \(\left| {{x^2} – 4x + 3} \right| = x + 3\) có nghiệm \(x = 0,\,\,x = 5\)
Suy ra
\(\begin{array}{l}S = \int\limits_0^1 {\left( { – {x^2} + 5x} \right)dx + \int\limits_1^3 {\left( {{x^2} – 3x + 6} \right)dx} } + \int\limits_3^5 {\left( { – {x^2} + 5x} \right)dx} \\ = \frac{{109}}{6}\end{array}\)
Câu 2. Diện tích hình phẳng được giới hạn bởi hai đồ thị hàm số \(y = 2{x^3} – 3{x^2} + 1\) và \(y = {x^3} – 4{x^2} + 2x + 1\) là
A. \(\frac{{37}}{{13}}\)
B. \(\frac{{37}}{{12}}\)
C. \(3\)
D. \(4\)
Hướng dẫn giải
Ta có \(2{x^3} – 3{x^2} + 1 = {x^3} – 4{x^2} + 2x + 1 \Leftrightarrow \left[ \begin{array}{l}x = – 2\\x = 0\\x = 1\end{array} \right.\)
Nên
\(\begin{array}{l}S = \int\limits_{ – 2}^1 {\left| {{x^3} + {x^2} – 2x} \right|dx} \\ = \left| {\int\limits_{ – 2}^0 {({x^3} + {x^2} – 2x)dx} } \right| + \left| {\int\limits_0^1 {({x^3} + {x^2} – 2x)dx} } \right|\end{array}\)
\( = \left| {\left. {\left( {\frac{{{x^4}}}{4} + \frac{{{x^3}}}{3} – {x^2}} \right)} \right|_{ – 2}^0} \right| + \left| {\left. {\left( {\frac{{{x^4}}}{4} + \frac{{{x^3}}}{3} – {x^2}} \right)} \right|_0^1} \right| = \frac{{37}}{{12}}\)
Câu 3. Diện tích hình phẳng giới hạn bởi các đồ thị hàm số $y = {x^2};\,\,y = \frac{1}{{27}}{x^2};\,\,y = \frac{{27}}{x}$ bằng
A. $27\ln 2$
B. $27\ln 3$
C. $28\ln 3$
D. $29\ln 3$
Hướng dẫn giải
Xét các pthđgđ
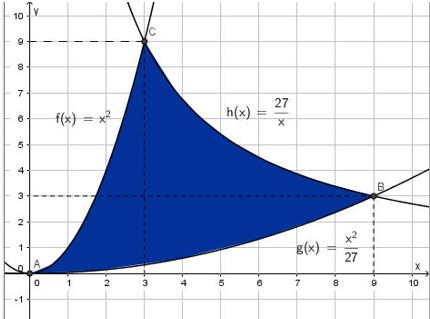
$\begin{array}{l}{x^2} – \frac{{{x^2}}}{{27}} = 0\\ \Rightarrow x = 0;{x^2} – \frac{{27}}{x} = 0\\ \Rightarrow x = 3;\frac{{{x^2}}}{{27}} – \frac{{27}}{x} = 0\\ \Rightarrow x = 9\end{array}$
Câu 4. $S = \int\limits_0^3 {\left( {{x^2} – \frac{{{x^2}}}{{27}}} \right)} dx + \int\limits_3^9 {\left( {\frac{{27}}{x} – \frac{{{x^2}}}{{27}}} \right)dx = 27\ln 3} $Hình phẳng giới hạn bởi đồ thị hàm số $(C):y = \frac{{ – {x^2} + 4x – 4}}{{x – 1}}$ , tiệm cận xiêm của $(C)$ và hai đường thẳng $x = 0,x = a{\rm{ }}(a < 0)$ có diện tích bằng $5$ Khi đó $a$ bằng
A. $1 – {e^5}$
B. $1 + {e^5}$
C. $1 + 2{e^5}$
D. $1 – 2{e^5}$
Hướng dẫn giải
Ta có
$TCX:y = – x + 3$
Nên $S(a) = \int\limits_a^0 {\left( { – \frac{1}{{x – 1}}} \right)} dx = \int\limits_0^a {\left( {\frac{1}{{x – 1}}} \right)} dx = \left. {\ln \left| {x – 1} \right|} \right|_0^a = \ln (1 – a)$
Suy ra $\ln (1 – a) = 5 \Leftrightarrow a = 1 – {e^5}$
Câu 5. Diện tích hình phẳng được giới hạn bởi đồ thị các hàm số y = f(x), y = g(x) liên tục trên đoạn ${\rm{[}}a;b{\rm{]}}$, trục hoành và hai đường thẳng \(x = a\), \(x = b\) được tính theo công thức
A. \(S = \int\limits_a^b {{{\left| {f(x) – g(x)} \right|}^2}dx.} \)
B. \(S = \int\limits_a^b {{\rm{[}}f(x) – g(x){\rm{]}}dx.} \)
C.\(S = \int\limits_a^b {\left| {f(x) – g(x)} \right|dx.} \)
D. \(S = \pi \int\limits_a^b {{{\left| {f(x) – g(x)} \right|}^2}dx.} \)
Hướng dẫn giải
Theo công thức (SGK cơ bản) ta có \(S = \int\limits_a^b {\left| {f(x) – g(x)} \right|dx.} \)
Câu 6. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = \sqrt x \) , trục hoành và hai đường thẳng \(x = 1\), \(x = 4\) là
A. \(4\)
B. \(\frac{{14}}{5}\)
C. \(\frac{{13}}{3}\)
D. \(\frac{{14}}{3}\)
Hướng dẫn giải
Ta có \(\sqrt x \ge 0\)trên đoạn ${\rm{[1}};4]$ nên $S = \int\limits_1^4 {\left| {\sqrt x } \right|dx = } \int\limits_1^4 {\sqrt x dx} = \frac{2}{3}\left. {{x^{\frac{3}{2}}}} \right|_1^4 = \frac{{14}}{3}$
Câu 7. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = {x^3} – 3{x^2}\) , trục hoành và hai đường thẳng \(x = 1\), \(x = 4\) là
A. \(\frac{{53}}{4}\)
B. \(\frac{{51}}{4}\)
C. \(\frac{{49}}{4}\)
D. \(\frac{{25}}{2}\)
Hướng dẫn giải
Ta có \({x^3} – 3{x^2} = 0 \Leftrightarrow x = 3 \in {\rm{[}}1;4]\)
Khi đó diện tích hình phẳng là
$\begin{array}{l}S = \int\limits_1^4 {\left| {{x^3} – 3{x^2}} \right|} dx\\ = \left| {\int\limits_1^3 {({x^3} – 3{x^2}} )dx} \right| + \left| {\int\limits_3^4 {({x^3} – 3{x^2}} )dx} \right|\\ = \left| {\left. {\left( {\frac{{{x^4}}}{4} – {x^3}} \right)} \right|_1^3} \right| + \left| {\left. {\left( {\frac{{{x^4}}}{4} – {x^3}} \right)} \right|_3^4} \right|\\ = 6 + \frac{{27}}{4} = \frac{{51}}{4}\end{array}$
Câu 8. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = \cos 2x\) , trục hoành và hai đường thẳng \(x = 0,x = \frac{\pi }{2}\) là
A. 1
B. 2
C. 3
D. 4
Hướng dẫn giải
Ta có \(\cos 2x = 0 \Leftrightarrow x = \frac{\pi }{4} \in {\rm{[0;}}\frac{\pi }{2}{\rm{]}}\)
Nên
\(\begin{array}{l}S = \int\limits_0^{\frac{\pi }{2}} {\left| {\cos 2x} \right|dx} \\ = \left| {\int\limits_0^{\frac{\pi }{4}} {\cos 2xdx} } \right| + \left| {\int\limits_{\frac{\pi }{4}}^{\frac{\pi }{2}} {\cos 2xdx} } \right|\\ = \left| {\left. {\left( {\frac{1}{2}\sin 2x} \right)} \right|_0^{\frac{\pi }{4}}} \right| + \left| {\left. {\left( {\frac{1}{2}\sin 2x} \right)} \right|_{\frac{\pi }{4}}^{\frac{\pi }{2}}} \right| = 1\end{array}\)
Hy vọng với bài viết ứng dụng tích phân ở trên sẽ hữu ích với các em. Những phản hồi về bài viết cũng như góp y vui lòng để lại dưới bình luận sẽ được giải đáp cho em sớm nhất. Chúc em học tốt